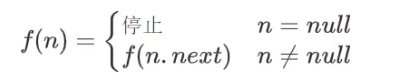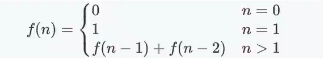数据结构与算法 数组 在计算机科学中,数组是由一组元素(值或变量)组成的数据结构,每个元素有至少一个索引或键来标识
因为数组内的元素是连续存储的,所以数组中元素的地址,可以通过其索引计算出来,例如:
知道了数组的数据起始地址BaseAddress,就可以由公式BaseAddress+i * size十算出索引i元素的地址·
i即索引,在Java、c等语言都是从0开始
size是每个元素占用字节,例如int 占4, double 占8
空间占用 Java中数组结构为
8字节 markword
4字节class指针(压缩class指针的情况)
4字节数组大小(决定了数组最大容量是232)
·数组元素+对齐字节(java中所有对象大小都是8字节的整数倍12,不足的要用对齐字节补足)
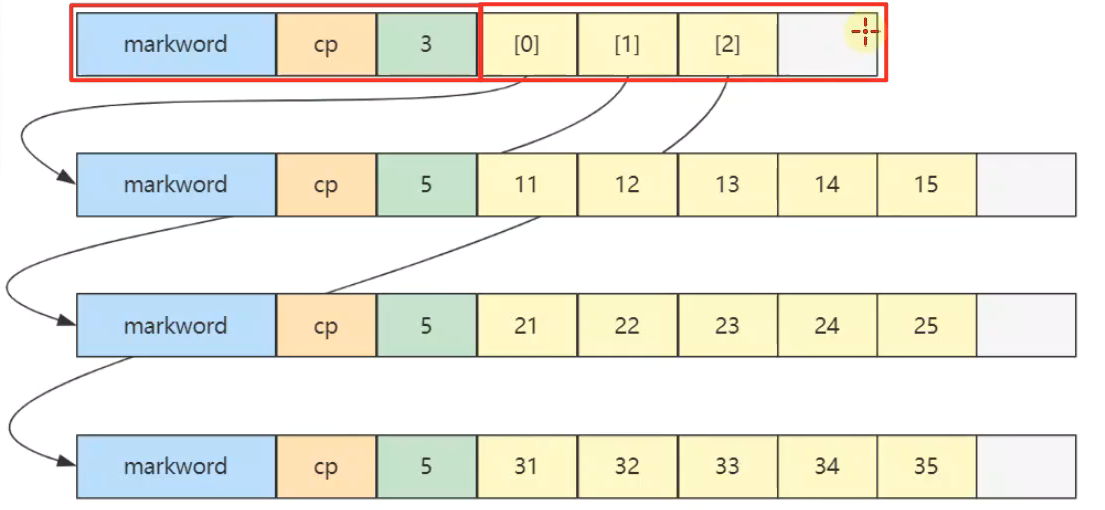
二维数组的内存图为
二维数组占32个字节,其中 array[0], array[1], array[2]三个元素分别保存了指向三个一维数组的引用
三个一维数组各占40个字节
它们在内层布局上是连续的
链表 在计算机科学中,链表是数据元素的线性集合,其每个元素都指向下一个元素,元素存储上并不连续
单向链表,每个元素只知道其下一个元素是谁
双向链表,每个元素知道其上一个元素和下一个元素
循环链表,通常的链表尾节点tail指向的都是null,而循环链表的tail指向的是头节点head
链表内还有一种特殊的节点称为哨兵(Sentinel)节点,也叫做哑元(Dummy)节点,.它不存储数据,通常用作头尾,用来简化边界判断,如下图所示
性能 随机访问
根据index查找,时间复杂度O(n)
插入或删除
起始位置:O(1)
结束位置:如果已知tail尾节点是O(1),不知道tail尾节点是O(n)
中间位置:根据index查找时间+O(1)
遍历链表的几种方法
遍历打印输出,直接在控制台
```java1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 2. 利用Consumer来进行自定义式的函数式接口 ```java public void loop(Consumer<Integer> consumer){ Node pointer=head; while (pointer!=null){ consumer.accept(pointer.value); pointer=pointer.next; } } 当使用时,可以这么使用 SinglyLinkedList list=new SinglyLinkedList(); list.addFirst(1); list.addFirst(2); list.addFirst(3); list.addFirst(4); list.loop(value->{ System.out.println(value); });
链表实现Iterable接口实现hasNext()方法与next()方法
```java iterator() {() { //是否还有下一个节点1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 ### 双向链表 双向链表存在于两个哨兵,一个是头head,另一个是尾tail用法和单向链表差不多,就是在插入删除的时候,指针变动的更频繁了 ### 环形链表 双向环形链表带哨兵,这时哨兵既作为头,也作为尾  ## 递归 计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集 例如: ```java voidf(Node node){ if(node==null){ return; } f(node.next); }
自己调用自己,如果说每个函数对应着一种解决方案,自己调用自己意味着解决方案是一样的(有规律的)
每次调用,函数处理的数据会较上次缩减(子集),而且最后会缩减至无需继续递归
内层函数调用(子集处理)完成,外层函数才能算调用完成
思路
1.确定能否使用递归求解
上述的链表的递推关系为:
深入到最里层叫做递
从最里层出来叫做归
在递的过程中,外层函数内的局部变量(以及方法参数)并未消失,归的时候还可以用到
插入排序的递归写法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 package DataStructure;import java.util.Arrays;public class InsertSort { public static void main (String[] args) { int a[] = {1 , 7 , 8 , 3 , 6 , 2 , 0 , 2 , 9 }; sort(a); Arrays.stream(a).forEach(System.out::println); } public static void sort (int a[]) { insertion(a, 0 ); } public static void insertion (int a[], int low) { if (low == a.length) { return ; } int temp = a[low]; int i = low - 1 ; while (i >= 0 && a[i] > temp) { a[i + 1 ] = a[i]; i--; } if (i + 1 != low) { a[i+1 ] = temp; } insertion(a, low + 1 ); } }
斐波那契数列的递归写法
之前的例子是每个递归函数只包含一个自身的调用,这称之为single recursion
如果每个递归函数例包含多个自身调用,称之为multi recursion
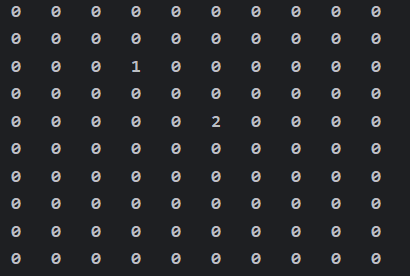
稀疏数组 出现的意义 当我们在做一个五子棋棋盘时(假设大小为10*10),实际是一个10* 10的矩阵,其中用0来表示棋盘上没有放棋子的位置,用1来表示放黑棋子的位置,用2来表示放白棋子的位置,利用Java语言我们可以得到改语句
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int [][] arr=new int [10 ][10 ]; for (int [] arr1:arr){ for (int i:arr1){ i=0 ; } } arr[2 ][3 ]=1 ; arr[4 ][5 ]=2 ; for (int i=0 ;i<10 ;i++){ for (int j=0 ;j<10 ;j++){ System.out.print(arr[i][j]+" " ); } System.out.println(); }
当我们要退出五子棋游戏,要存档时,我们是否要将整个棋盘存入到硬盘中?有没有解决方案
稀疏数组! 稀疏数组用于解决在一个二维数组中0的数量>其他值的数量的情况,或特殊值数量小于常见值,用于将二维数组压缩成一个小的二维数组
例如:
将上述的二维数组压缩为稀疏数组为
这样将上面一个大二维数组压缩成一个3*3的小二维数组,涉及到上述的场景中当要恢复棋盘时,我们也要根据所读的稀疏数组来将数组转化为原二维数组
如何实现稀疏数组 首先先定义原数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int [][] arr=new int [10 ][10 ];for (int [] arr1:arr){ for (int i:arr1){ i=0 ; } } arr[2 ][3 ]=1 ; arr[4 ][5 ]=2 ; for (int i=0 ;i<10 ;i++){ for (int j=0 ;j<10 ;j++){ System.out.print(arr[i][j]+" " ); } System.out.println(); }
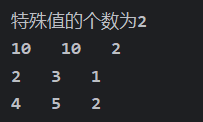
二维数组数组转化为稀疏数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 int count = 0 ; for (int i = 0 ; i < 10 ; i++) { for (int j = 0 ; j < 10 ; j++) { if (arr[i][j] != 0 ) { count++; } } } System.out.println("特殊值的个数为" +count); int [][] arr2 = new int [count + 1 ][3 ]; int index = 1 ; arr2[0 ][0 ] = 10 ; arr2[0 ][1 ] = 10 ; arr2[0 ][2 ] = count; for (int i = 0 ; i < 10 ; i++) { for (int j = 0 ; j < 10 ; j++) { if (arr[i][j] != 0 ) { arr2[index][0 ] = i; arr2[index][1 ] = j; arr2[index][2 ] = arr[i][j]; index++; } } } for (int i = 0 ; i < arr2.length; i++) { System.out.print(arr2[i][0 ] + " " + arr2[i][1 ] + " " + arr2[i][2 ] + " " ); System.out.println(); }
将稀疏数组转化为原二维数组
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 int index1 = arr2[0 ][0 ];int index2 = arr2[0 ][1 ];int [][] TwoArray = new int [index1][index2];for (int i = 0 ; i < index1; i++) { for (int j = 0 ; j < index2; j++) { TwoArray[i][j] = 0 ; } } for (int i = 1 ; i < arr2.length; i++) { TwoArray[arr2[i][0 ]][arr2[i][1 ]] = arr2[i][2 ]; } for (int i = 0 ; i < index1; i++) { for (int j = 0 ; j < index2; j++) { System.out.print(TwoArray[i][j] + " " ); } System.out.println(); }
队列 队列和我们日常排队一样,有队头和队尾 队列遵循以下特点
队列数据结构具有以下几个特点:
先进先出(FIFO):队列遵循先进先出的原则,也就是最先插入的元素会最先被移除,新元素插入的位置为队列的尾部,而移除元素发生在队列的头部。
有限容量:队列具有一定的容量限制,即队列中可以存放的元素数量是有限的。当队列已满时,继续插入元素会导致队列溢出。
插入和删除操作:队列支持在队尾插入元素的操作,通常称为入队(enqueue)或添加(enqueue)操作。同时,队列也支持在队头删除元素的操作,通常称为出队(dequeue)或移除(dequeue)操作。
提供队列大小和状态检查:队列通常提供方法来获取队列的当前大小,即队列中元素的数量。此外,队列还提供方法来检查队列是否为空或已满。
高效性:队列的实现通常能够提供高效的入队和出队操作。具体实现方式可能会根据不同的数据结构选择不同的策略,例如使用数组、链表、堆等。
多线程安全:某些队列数据结构支持多线程环境下的并发操作,并提供线程安全的方法,以确保在并发情况下的一致性和可靠性。
队列数据结构在很多场景中都很有用,特别适合于需要按照特定顺序处理数据的情况,例如任务调度、消息传递、缓冲区等。它的特点使得其在多种应用中都能得到广泛应用。
因为队列的输出、输入是分别从前后端来处理,因此需要两个变量front及rear分别记录队列前后端的下标,front 会随着数据输出而改变,而rear则是随着数据输入而改变,如图所示:
front=rear说明队列为空,fear=maxsize-1证明队列已满
可由数组得到队列:
普通数组队列 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 class ArrayQueue { private int maxSize; private int front; private int rear; private int [] arr; public ArrayQueue (int arrMaxSize) { maxSize = arrMaxSize; arr = new int [arrMaxSize]; int front = -1 ; int rear = -1 ; } public boolean isFull () { return rear == maxSize - 1 ; } public boolean isEmpty () { return front == rear; } public void addQueue (int n) { if (isFull()) { System.out.println("队列满不可加入数据" ); return ; } rear++; arr[rear] = n; } public int getQueue () { if (isEmpty()) { throw new RuntimeException ("队列空,不可获取数据" ); } int result; front++; result=arr[front]; arr[front]=0 ; return result; } }
环形数组队列 上述队列容易出现队列仅可用一次,不可重复使用的情况,所以不得不用环形队列增加复用
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 import com.sun.jmx.remote.internal.ArrayQueue;public class ArrayQueueDemo { public static void main (String[] args) { class ArrayQueue { private int maxSize; private int front; private int rear; private int [] arr; public ArrayQueue (int arrMaxSize) { maxSize = arrMaxSize; arr = new int [arrMaxSize]; int front = 0 ; int rear = 0 ; } public boolean isFull () { return (rear + 1 ) % maxSize == front; } public boolean isEmpty () { return front == rear; } public void addQueue (int n) { if (isFull()) { System.out.println("队列满不可加入数据" ); return ; } arr[rear] = n; rear = (rear + 1 ) % maxSize; } public int getQueue () { if (isEmpty()) { throw new RuntimeException ("队列空,不可获取数据" ); } int result; result = arr[front]; arr[front] = 0 ; front = (front + 1 ) % maxSize; return result; } public void showQueue () { if (isEmpty()) { throw new RuntimeException ("队列为空" ); } for (int i = front; i < front + size(); i++) { System.out.print(arr[i % maxSize] + " " ); } } public int size () { return (rear + maxSize - front) % maxSize; } } ArrayQueue arrayQueue = new ArrayQueue (10 ); arrayQueue.addQueue(10 ); arrayQueue.addQueue(10 ); arrayQueue.addQueue(10 ); arrayQueue.addQueue(10 ); arrayQueue.showQueue(); arrayQueue.getQueue(); arrayQueue.showQueue(); } }
单向链表 java中实现链表的方式与C类似,C中使用指针将下一个节点的地址指向出来,而java中是将节点对象以成员变量引用的方式引用到到对象中。
原理类似直接看代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 class HeroNode { int no; String name; String nickName; HeroNode next; public HeroNode () { } public HeroNode (int no, String name, String nickName) { this .no = no; this .name = name; this .nickName = nickName; } @Override public String toString () { return "HeroNode{" + "no=" + no + ", name='" + name + '\'' + ", nickName='" + nickName + '\'' + '}' ; } } class SingleLinkedList { private HeroNode head = new HeroNode (0 , "" , "" ); public void add (HeroNode heroNode) { HeroNode tmp = head; while (true ) { if (tmp.next==null ) { tmp.next=heroNode; return ; } tmp=tmp.next; } } public void showLinkedList () { if (head.next==null ) { System.out.println("该链表为空,请插入数据" ); return ; } HeroNode tmp=head; while (tmp.next!=null ){ System.out.println(tmp.next); tmp=tmp.next; } } }
上述代码中对链表的遍历以及尾插法插入数据都与C中的链表类似,我们来测试看看
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public class LinkedListDemo { public static void main (String[] args) { HeroNode h1=new HeroNode (1 ,"宋江" ,"及时雨" ); HeroNode h2=new HeroNode (2 ,"卢俊义" ,"玉麒麟" ); HeroNode h3=new HeroNode (3 ,"吴用" ,"智多星" ); HeroNode h4=new HeroNode (4 ,"林冲" ,"豹子头" ); SingleLinkedList list=new SingleLinkedList (); list.add(h1); list.add(h2); list.add(h3); list.add(h4); list.showLinkedList(); } }
按号插入节点 当在链表存储时,我们要保证节点不重复并且,做到按照某种规则去按顺序链接,我们可以使用以下方法插入
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 public void addByOrder (HeroNode heroNode) { HeroNode tmp = head; if (head.next == null ) { tmp.next = heroNode; System.out.println("链表为空,直接插入头结点后" ); return ; } while (true ) { if (tmp.next == null ) { System.out.println("插入成功,插入到了链尾中" ); tmp.next = heroNode; return ; } if (heroNode.no > tmp.no) { if (heroNode.no == tmp.next.no){ System.out.println("插入失败,NO重复" ); return ; } if (heroNode.no < tmp.next.no) { heroNode.next = tmp.next; tmp.next = heroNode; System.out.println("插入成功" ); return ; } } tmp = tmp.next; } }
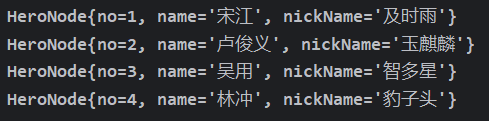
此时我们打乱插入顺序,并且按照no进行排序插入,此时我们遍历后可以获得
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public class LinkedListDemo { public static void main (String[] args) { HeroNode h1 = new HeroNode (1 , "宋江" , "及时雨" ); HeroNode h2 = new HeroNode (2 , "卢俊义" , "玉麒麟" ); HeroNode h3 = new HeroNode (3 , "吴用" , "智多星" ); HeroNode h4 = new HeroNode (4 , "林冲" , "豹子头" ); SingleLinkedList list = new SingleLinkedList (); list.addByOrder(h2); list.addByOrder(h1); list.addByOrder(h4); list.addByOrder(h3); list.showLinkedList(); } }
遍历后我们发现还是按照顺序遍历
反转链表 给哥们整吐了,但是解题思路是真的好
反转链表, 例如链表是 1 2 3 4 链表 ,经过翻转后为 4 3 2 1 ,看上去很简单,实则很恶心
以下是其算法
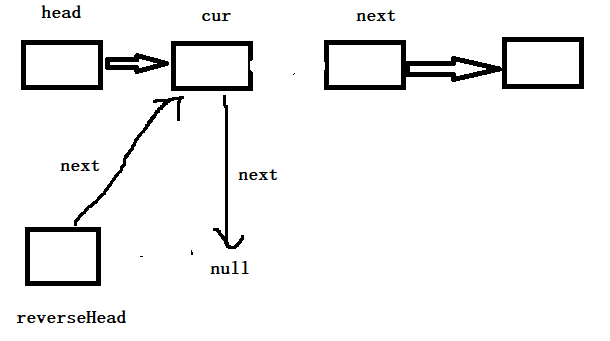
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 public void reverse () { LinkedNode reverseHead = new LinkedNode (0 ); if (this .head.next == null || this .head.next.next == null ) { System.out.println("该链表为空或该链表长度为1不必翻转" ); } LinkedNode cur = this .head.next; LinkedNode next = null ; while (cur != null ) { next = cur.next; cur.next = reverseHead.next; reverseHead.next = cur; cur = next; } head.next = reverseHead.next; }
算法执行过程:
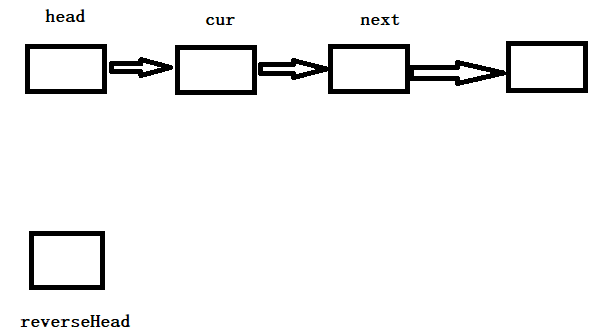
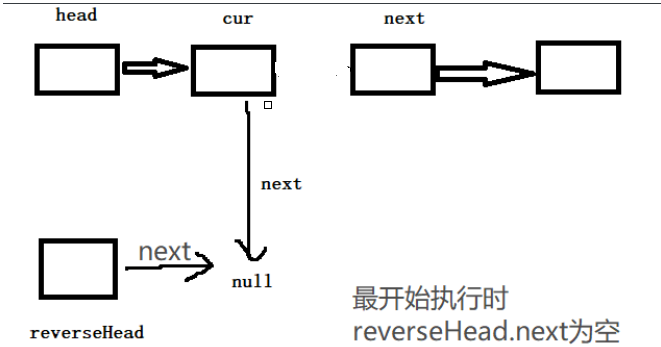
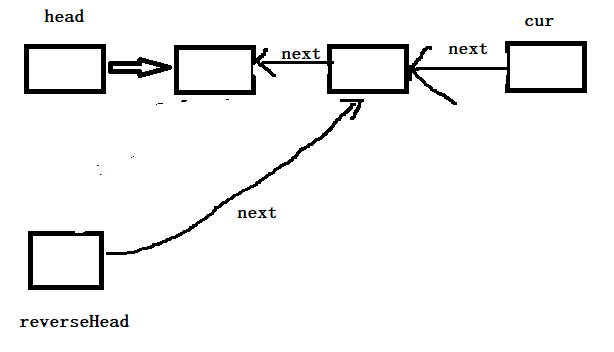
一开始是这样的(四个为例)
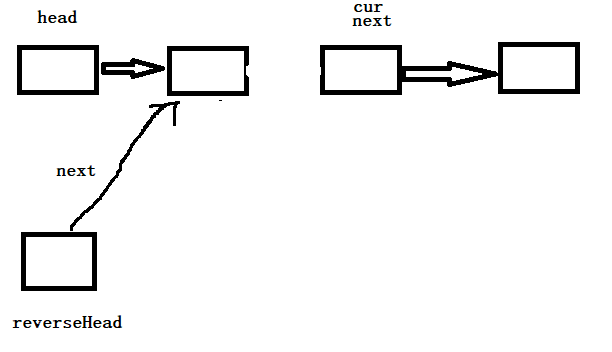
执行 cur.next = reverseHead.next ;后
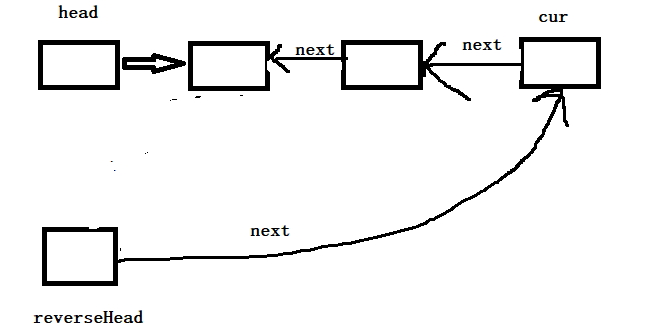
执行 reverseHead.next = cur后
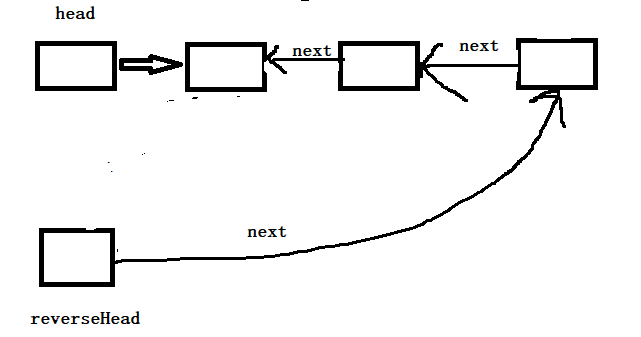
执行 cur = next 后
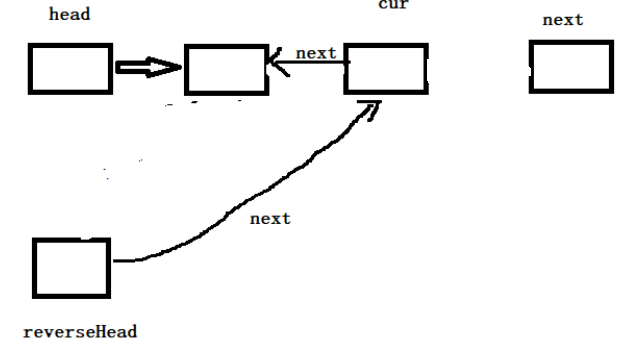
第二次执行 cur.next = reverseHead.next后
第二次执行 reverseHead.next = cur后 **
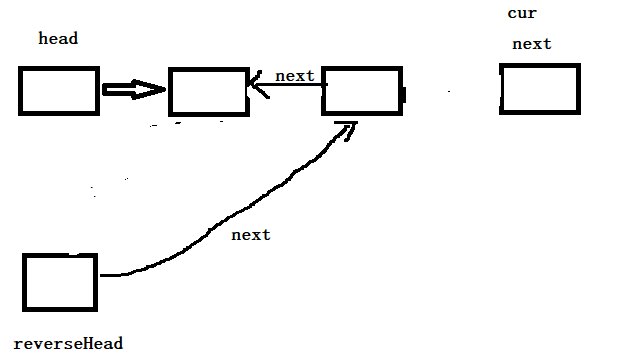
第二次执行 cur = next 后
第三次执行 cur.next = reverseHead.next后
第三次执行 reverseHead.next = cur后 **
第三次执行 cur = next 后(cur指针也为空了)
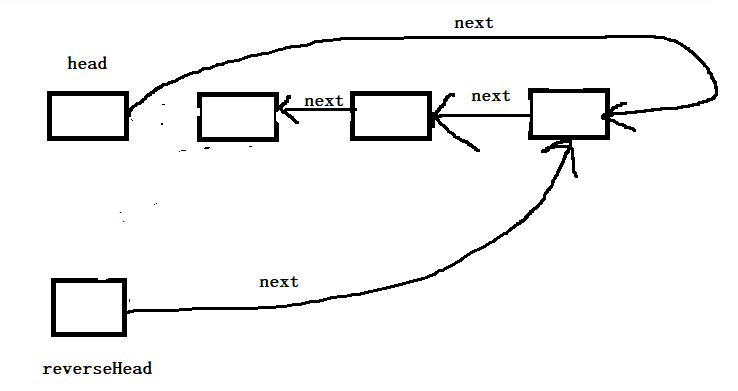
跳出循环后执行为
实现了链表的翻转(真的牛逼)!!!!
约瑟夫环算法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 public class Josephu { public static void main (String[] args) { CircleLinkedList circleLinkedList = new CircleLinkedList (); circleLinkedList.play(5 , 2 ); } } class CircleLinkedList { private Boy first = new Boy (-1 ); public void addBoy (int num) { if (num < 1 ) { System.out.println("num值不正确" ); return ; } Boy curBoy = null ; for (int i = 1 ; i <= num; i++) { Boy boy = new Boy (i); if (i == 1 ) { first = boy; first.setNext(boy); curBoy = boy; } else { curBoy.setNext(boy); boy.setNext(first); curBoy = boy; } } } public void play (int num, int count) { this .addBoy(num); if (num == 1 ) { System.out.println(this .first); } int index = 1 ; while (this .first.next != this .first) { if (index == count - 1 ) { System.out.println(this .first.next.no); index = 0 ; this .first.next = this .first.next.next; } this .first = this .first.next; index++; } System.out.println(this .first.no); } } class Boy { Integer no; Boy next; public Boy (int no) { this .no = no; } public Integer getNo () { return no; } public void setNo (Integer no) { this .no = no; } public Boy getNext () { return next; } public void setNext (Boy next) { this .next = next; } @Override public String ztoString () { return "Boy{" + "no=" + no + '}' ; } }
回文数 什么是回文数: 121 ,212 ,1221,2112 但-121……就不是
解题思路:
首先 ,我们可以判断负数就不是回文数,并且 我们可以了解到回文数的性质:
abcdcba,如果a是0的话,即数字的最后一位为0,难么首位就是0,但数字的个位是不会是0的,所以 x%10==0时,该数字则不是回文数,但如果如果这个数本身就是0的话,他也是回文数,所以 a<0|| (a >0&&a%10==0)则这个数就不是回文数
其次,深入了解回文数的性质,如何去判断abcdcba,我们可以通过取余的方式来获取到最后一位数字,那如何每次遍历都获取到最后一位数字呢?在每一次遍历的同时给该数进行整除 ,那获取到每一位最后一个数字,如何拼接成数字呢?对每一次取余下来的数加上之前的数*10,例如
1 2 x=0 + 1221 %10 ; x=1 *10 +2 ;
那要什么时候停止遍历呢? 我们可以得知,拼接数和原先的数相比 拼接数会是<原数的,但当拼接数==原来数 或 拼接数>原来数()时,就要停止遍历,再往下遍历,肯定就会不回文了,所以上述的判断,拼接数什么时候等于原来数呢?(该数一共有偶数位时)什么时候大于原来数呢?(该数是奇数位时),所以当我们遍历过后,去判断拼接数和原来数时我们可以这样判断 ,如果是回文数则符合下述要求
1 pinjieNum==x||pinjieNum/10 ==x
具体算法如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { public boolean isPalindrome (int x) { if (x<0 ||(x>0 &&x%10 ==0 )){ return false ; } int huiwenshu=0 ; while (x>huiwenshu){ huiwenshu=huiwenshu*10 +x%10 ; x/=10 ; } return huiwenshu==x||huiwenshu/10 ==x; } }
栈 先进后出
前缀(波兰表达式)、中缀、后缀表达式(逆波兰表达式)
前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前
举例说明:(3+4)×5-6对应的前缀表达式就是-×+3 4 5 6
逆波兰表达式算法:
逆波兰表达式(后缀表达式): 我们可以通过一个数的逆波兰表达式来更快速的设计出一个计算机。
给定一个逆波兰表达式,获取他的值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 class Solution { public int evalRPN (String[] tokens) { Stack<String> stack= new Stack <String>(); for (String s:tokens){ if (!isOper(s)){ stack.push(s); }else { int num2= Integer.parseInt(stack.pop()); int num1= Integer.parseInt(stack.pop()); String result= String.valueOf(cal(num1,num2,s)); stack.push(result); } } return Integer.parseInt( stack.pop()); } public static boolean isOper (String s) { return s.equals("+" )||s.equals("-" )||s.equals("*" )||s.equals("/" ); } public static Integer cal (int num1,int num2,String oper) { switch (oper){ case "+" : return num1+num2; case "-" : return num1-num2; case "*" : return num1*num2; case "/" : return num1/num2; } return 0 ; } }
回溯 迷宫算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 public class MIGong { public static void main (String[] args) { int [][] map = new int [8 ][7 ]; for (int i = 0 ; i < 8 ; i++) { map[i][0 ] = 1 ; map[i][6 ] = 1 ; } for (int i = 0 ; i < 7 ; i++) { map[0 ][i] = 1 ; map[7 ][i] = 1 ; } map[3 ][1 ] = 1 ; map[3 ][2 ] = 1 ; map[5 ][3 ]=1 ; map[5 ][4 ]=1 ; map[5 ][5 ]=1 ; setWay(map, 1 , 1 ); for (int i = 0 ; i < 8 ; i++) { for (int j = 0 ; j < 7 ; j++) { System.out.print(map[i][j] + " " ); } System.out.println(); } } public static boolean setWay (int [][] map, int i, int j) { if (map[6 ][5 ] == 2 ) { return true ; } else { if (map[i][j] == 0 ) { map[i][j] = 2 ; if (setWay(map, i + 1 , j)) { return true ; } if (setWay(map, i, j + 1 )) { return true ; } if (setWay(map, i - 1 , j)) { return true ; } if (setWay(map, i, j - 1 )) { return true ; } else { map[i][j] = 3 ; return false ; } } else { return false ; } } } }
八皇后算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 public class Quuen8 { int max = 8 ; static int count = 0 ; int [] arr = new int [max]; public static void main (String[] args) { Quuen8 quuen8 = new Quuen8 (); quuen8.putQuuen8(0 ); System.out.println("一共有" +count+"种解法" ); } private void putQuuen8 (int n) { if (n == max) { print(); return ; } for (int i = 0 ; i < max; i++) { arr[n] = i; if (judge(n)) { putQuuen8(n+1 ); } } } private boolean judge (int n) { for (int i = 0 ; i < n; i++) { if (arr[i] == arr[n] || Math.abs(n - i) == Math.abs(arr[n] - arr[i])) { return false ; } } return true ; } private void print () { for (int i = 0 ; i < arr.length; i++) { System.out.print(arr[i] + " " ); } count++; System.out.println(); } }
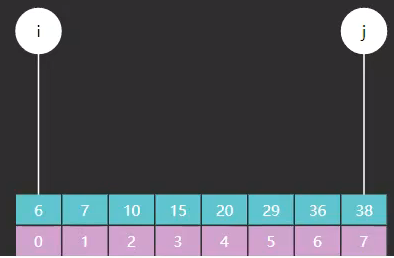
查找算法 二分查找 二分查找的过程
初始化指针i j 且i=0 作为最左边的索引指针 , j=int[].length-1作为最后边的索引指针
首先要判断 i j 索引所在数组的位置上的值是否和目标值相等
若相等则直接返回其索引值
算出 i j 索引的中间索引 m,并比较其所代表的值 temp与目标值 target之间的区别
若temp>target则让 j移动到 m左边的一个位置 m-1
若temp<target则让i 移动到 m右边的一个位置 m+1
若temp=target则直接返回m (成功找到)
执行 重复执行 2 、3步骤
若i=j时还未任何值返回,则返回-1 (代表未 查询到)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public static int binarySeachBasic (int [] a, int target) { int i = 0 ; int j = a.length - 1 ; while (i <= j) { int m = (i + j) >>>1 ; if (a[i]==target){ return i; } if (a[j]==target){ return j; } if (target < a[m]) { j = m - 1 ; } else if (target > a[m]) { i = m + 1 ; } else { return m; } } return -1 ; }
排序算法 冒泡排序 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 public class BubbleSort { static int count = 0 ; public static void sort (int [] arr) { boolean flag = false ; for (int i = 0 ; i < arr.length; i++) { for (int j = 0 ; j < arr.length - i - 1 ; j++) { if (arr[j] > arr[j + 1 ]) { int temp = arr[j]; flag = true ; arr[j] = arr[j + 1 ]; arr[j + 1 ] = temp; } count++; } if (!flag) { break ; } else { flag = false ; } } } public static void main (String[] args) { int [] arr = {3 , 2 , 1 , 5 , 6 , 4 , 8 , 10 }; sort(arr); System.out.println("共排序" + count + "次" ); System.out.println("共排序" + count + "次" ); for (int i : arr) { System.out.println(i); } } }
选择排序 选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,再依规定交换位置后达到排序的目的。选择排序(select sorting)也是一种简单的排序方法。它的基本思想是:第一次从arr[o]arr[n-1]中选取最办值,与arr[o]交换,第二次从arr[1]arr[n-1]中选取最小值,与arr[1]交换,第三次从arr[2]arr[n-1]中选取最小值,与arr[2]交换,…,第i次从arr[i-1]arr[n-1]中选取最小值,与arr[i-1]交换,…,第n-1次从arr[n-2]~arr[n-1]中选取最小值,与arr[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public static void SelectSort (int [] arr) { for (int i = 0 ; i < arr.length; i++) { for (int j = i; j < arr.length; j++) { int minKey = arr[i]; if (minKey > arr[j]) { int temp = arr[j]; arr[j] = minKey; minKey = temp; } count++; arr[i]=minKey; } } }
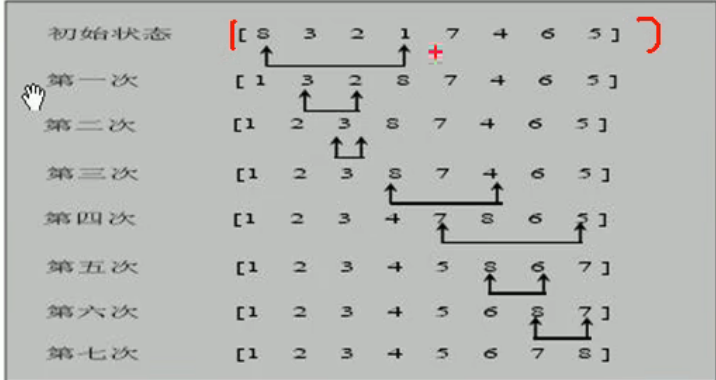
插入排序 插入式排序属于内部排序法,是对于欲排序的元素以插入的方式找寻该元素的适当位置,以达到排序的目的。
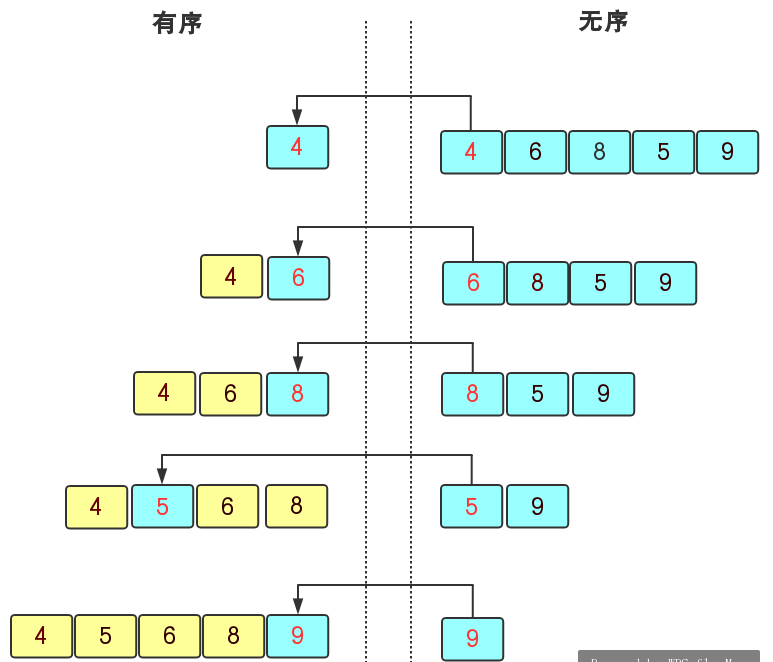
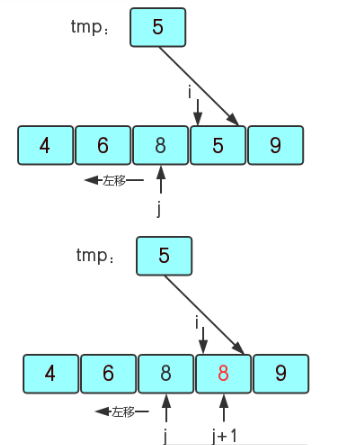
算法实现:直接插入排序是将无序序列中的数据插入到有序的序列中,在遍历无序序列时,首先拿无序序列中的首元素去与有序序列中的每一个元素比较并插入到合适的位置,一直到无序序列中的所有元素插完为止。对于一个无序序列arr{4,6,8,5,9}来说,我们首先先确定首元素4是有序的,然后在无序序列中向右遍历,6大于4则它插入到4的后面,再继续遍历到8,8大于6则插入到6的后面,这样继续直到得到有序序列{4,5,6,8,9}。
1 2 3 4 5 6 7 8 9 10 11 12 13 public static void InsertSort (int [] arr) { int temp; int i; int j; for (i=1 ;i<arr.length;i++){ temp=arr[i]; for (j=i-1 ;j>=0 &&arr[j]>temp;j--){ arr[j+1 ]=arr[j]; count++; } arr[j+1 ]=temp; } }
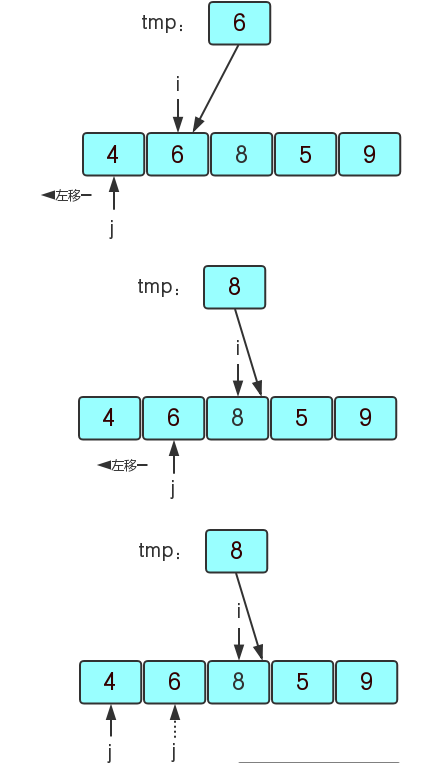
(1)我们用一个变量tmp存放关键字,因为我们先确定第一个元素是暂时有序的,所以tmp存放无序序列的第二个元素,然后i开始也为第二个元素的下标,j则为i-1,因为j要用有序的区域元素来与无序的区域元素比较。那么一开始i=1,tmp=6,j=0,因为6>4,所以6就不用进行插入;然后i向右走,i=2,tmp=arr[2]=8,j=i-1=1,8>6>4也不用插入
(2)i继续向右走,i=3,tmp=arr[3]=5,j=i-1=2,5<8则要将8给5所在的元素数据,j向左走继续遍历有序区域。
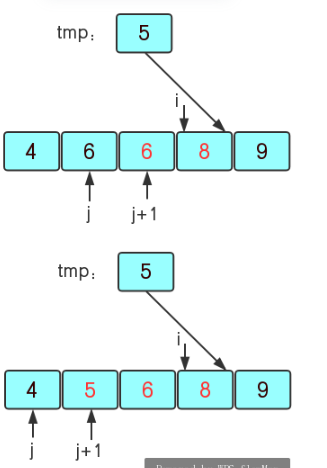
(3)当j向右走到6时发现6>tmp=5,所以将6给它右边的第一个值(j+1的位置),再继续遍历有序区域,j=0时发现4<5则j+1的位置就是5该在的位置那么就将tmp的值5给j+1的位置的元素的值。
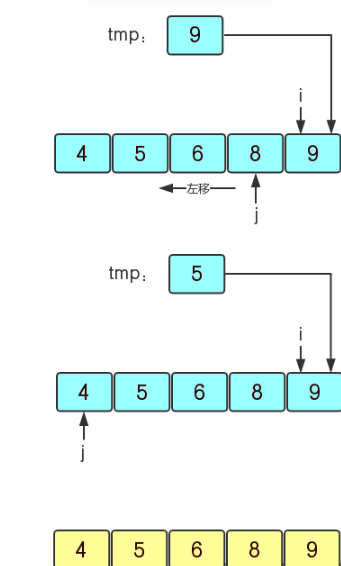
(4)再继续上面的操作,i最后到9发现比前面有序区域的元素都大,则不用再插入了,这样就得到了一个有序序列{4,5,6,8,9}。
希尔排序